Big O is basically a mathematical unit to describe the efficiency of algorithms. It is a language, which is used as a metric for comparing the efficiency of different algorithms.

Analogy

Let us try and understand this with the help of an example –

Consider I have a file that needs to be delivered to one of my friends on an urgent basis. Now the question is how do I deliver it? Now some of us have a direct answer to this question – E-mail.

But let’s say the size of the file is around 10TB, and the friend lives approximately 20 miles from my home. Consider this a life & death situation, will still your answer be E-mail? Because attaching a file this huge might require 2-3 days of time. The other answer to this particular question will be – Maybe I can use my car and deliver it to my friend by driving there.

Looking at the above example I think we have a fair amount of idea of what exactly is happening here. Based on our situation we change our answers, if the delivery of file is too important I shall not consider the resources like fuel, to stop me from delivering it.

What is Time & Space Complexity?

Considering the example above, Time complexity is the variation in time with the variation in input. Let me break it down a bit in technical terms –

E-mail (‘x’ sized file) – The time it takes to send a file through email, increases with an increase in the size of the file, i.e. it is dependent upon the size of the file. Thus the time complexity for this answer would be O(x), x being the size of the file.

Drive to the friend’s location – The time it takes to deliver a file by driving to a friends location is a constant. No matter how big or small the size of the file is it will take a fixed ‘N’ amount of time, where N is a constant. Thus, the size of the file does not matter so to deliver a file would take O(1).

In the example above, we discussed things around the time complexity of a problem. Similarly, for space complexity, the space required for an increase in input size is known as Space complexity.

Time complexity denotes the rate of increase in time, with an increase in the input size. This is not the exact time required by the algorithm.

Same goes for space complexity.

What is the difference between O, Ω & Ɵ?

To be very straightforward here, the only difference they have is in academic learnings. As per the industry standards, Big O is generally referred to as the Big Ɵ, of the academia.

• Big O – The upper bound on the time. It specifically says “The algorithm is at least as fast as O(N)”.
• Big Ω – The lower bound on the time. It specifically says “The algorithm cannot be faster than Ω(N)”.
• Big Ɵ – This means both O & Ω. This gives a tight bound on the runtime of the algorithm. An algorithm can only beƟ(N) if it has both O(N) & Ω(N).

What is the role of Constants?

We generally refrain ourselves, from using constants while defining the runtimes of our algorithm using constants, i.e. O(N) is as good as O(2N).

What are non-dominant terms and why do we drop them?

The non-dominant terms are the terms that in a way, play the role of constants. It’s just that the constant is not exactly known. For example –

• O(N² + N) becomes O(N²), as the other N is the size of the input and is not a dominant term.
• O(5*2^N + 10 N¹⁰) becomes O(2^N), as everything else is a constant (5 & 10) or a non-dominant term.

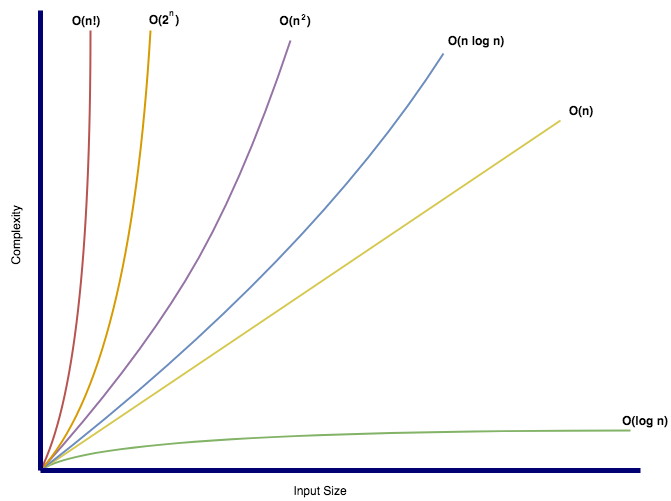
What is “log N” in runtimes?

The best example to understand this would be a binary search, where we divide the whole array into 2 parts and then continue our search with the rest of the array, reducing the size by half each time till we find the element.

The total time is then a matter of number of steps, we can take to bring N down to 1.

N=32
N=16 /*divide 32 by 2*/
N=8 /*divide 16 by 2*/
N=4 /*divide 8 by 2*/
N=2 /*divide 4 by 2*/
N=1 /*divide 2 by 2*/

We can see that this in reverse is what log represents.

• 2^k = N
• log₂ N = k – Here N is the size of the input, k is the number of steps required

For example : log₂ 32 = 5

What are Recursive runtimes?

Recursive runtimes in general, depend upon the depth it has created in recursion. Consider an example –

long cal(long num) { 
    if(num <= 1) {
        return 1;     
    }
    return cal(num - 1) * cal(num - 1); 
}

A lot of us might go straight to think this is O(N²), as the function is called twice recursively, but is it really so?

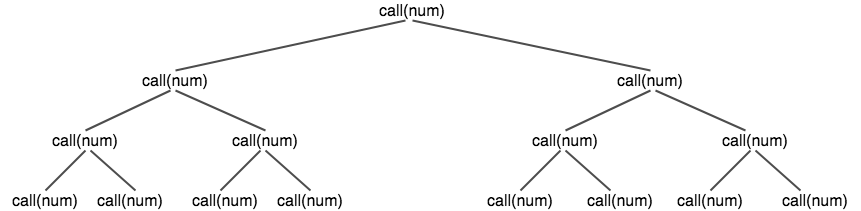
No, not really. This is the case of recursion, though, the function has been called twice, but this only happens the first time, the second time the 2 functions go ahead to call 4 functions collectively, and so on it grows, but there is a certain pattern in it. And the pattern is below –

2⁰ + 2¹ + 2² + 2³ + … + 2^N, which can be simply rewritten as (2^N+1 – 1).

A more general form for runtime would be – O(b^d), where “b” is the number of times the method as been called recursively inside itself, and “d” is the depth of the tree formed by recursion.

I hope this might have cleared a bit about the Big O notation and its usage. If you want to learn more, do post out comments, and I will try my best to answer your question.